Analytical Approaches for the Segmentation of the Zebrafish Brain Vasculature
Elisabeth C. Kugler, Elisabeth C. Kugler, Andrik Rampun, Andrik Rampun, Timothy J. A. Chico, Timothy J. A. Chico, Paul A. Armitage, Paul A. Armitage
Abstract
With advancements in imaging techniques, data visualization allows new insights into fundamental biological processes of development and disease. However, although biomedical science is heavily reliant on imaging data, interpretation of datasets is still often based on subjective visual assessment rather than rigorous quantitation. This overview presents steps to validate image processing and segmentation using the zebrafish brain vasculature data acquired with light sheet fluorescence microscopy as a use case.
Blood vessels are of particular interest to both medical and biomedical science. Specific image enhancement filters have been developed that enhance blood vessels in imaging data prior to segmentation. Using the Sato enhancement filter as an example, we discuss how filter application can be evaluated and optimized. Approaches from the medical field such as simulated, experimental, and augmented datasets can be used to gain the most out of the data at hand. Using such datasets, we provide an overview of how biologists and data analysts can assess the accuracy, sensitivity, and robustness of their segmentation approaches that allow extraction of objects from images. Importantly, even after optimization and testing of a segmentation workflow (e.g., from a particular reporter line to another or between immunostaining processes), its generalizability is often limited, and this can be tested using double-transgenic reporter lines. Lastly, due to the increasing importance of deep learning networks, a comparative approach can be adopted to study their applicability to biological datasets.
In summary, we present a broad methodological overview ranging from image enhancement to segmentation with a mixed approach of experimental, simulated, and augmented datasets to assess and validate vascular segmentation using the zebrafish brain vasculature as an example. © 2022 The Authors. Current Protocols published by Wiley Periodicals LLC.
Highlights
- Simulated, experimental, and augmented datasets provide an alternative to overcome the lack of segmentation gold standards and phantom models for zebrafish cerebrovascular segmentation.
- Direct generalization of a segmentation approach to the data for which it was not optimized (e.g., different transgenics or antibody stainings) should be treated with caution.
- Comparison of different deep learning segmentation methods can be used to assess their applicability to data. Here, we show that the zebrafish cerebral vasculature can be segmented with U-Net–based architectures, which outperform SegNet architectures.
INTRODUCTION
Abbreviations
| BA | basilar artery |
| CNR | contrast-to-noise ratio |
| CtA | central artery |
| dpf | days post fertilization |
| FWHM | full width at half-maximum |
| GF | general filtering |
| hpf | hours post fertilization |
| LSFM | light sheet fluorescence microscopy |
| MMCtA | middle mesencephalic central artery |
| PMBC | primordial midbrain channel |
| ROI | region of interest |
| SE | Sato enhancement |
Zebrafish as Preclinical Model in Cardiovascular Research
Vascular diseases are the leading cause of death worldwide (Feigin, Norrving, & Mensah, 2017; Lackland & Weber, 2015), whereas diseases of the central nervous system are associated with neurodegeneration, arteriovenous malformations, aneurysms, and stroke.
Zebrafish are commonly used to study embryonic development and disease due to their characteristics including high genomic similarity to humans, high progeny rates, and ex utero development (Bowley et al., 2021; Chico, Ingham, & Crossman, 2008; Gut, Reischauer, Stainier, & Arnaout, 2017). The availability of fluorescent transgenic reporter lines, combined with embryonic transparency, allows visualization of subcellular structures of interest with high specificity. For example, endothelial cells lining the vascular lumen can be visualized noninvasively in vivo (Lawson & Weinstein, 2002), allowing visualization of vascular anatomy with unprecedented spatial and temporal detail.
With the emergence of sophisticated microscopy techniques, such as light sheet fluorescence microscopy (LSFM), vascular information can not only be acquired with great anatomical detail but also over extended periods of time, such as hours to days (Huisken, Swoger, Del Bene, Wittbrodt, & Stelzer, 2004). Combining zebrafish fluorescent transgenic reporter lines and LSFM allows for acquiring data rich in anatomical depth, spatiotemporal resolution, and detail, enabling discovery and investigation of many biological processes (Bowley et al., 2021; Gut et al., 2017). Together, these advances mean that often it is no longer the experiments that are the limitations, but how to handle, analyze, and meaningfully interpret the acquired imaging datasets.
Challenges in Quantifying the Zebrafish Cranial Vasculature
Although certain characteristics of the cerebrovascular architecture may be obvious on visual inspection (such as missing or highly abnormal vessels), others may be too subtle for visual detection (such as diameter changes). Generally, 3D computational quantification of the vascular architecture is not only less labor-intensive but is also more comprehensive than manual assessments, providing measurements of volume, diameter, length, and branching (Kugler et al., 2022). Additionally, computational analysis is often more reproducible and sensitive than visual/manual assessment, requiring fewer animals.
In practice, before being able to quantify properties of objects/cells in 3D images, imaging data often need to be binarized, using a process called segmentation. In its simplest form, this first step toward computational data analysis extracts objects from grayscale or color images (i.e., in semantic segmentation; instance segmentation could indicate individual vascular trees). After segmentation, the image contains features of interest represented by a value of one, and everything else represented as zero. In the case of vascular segmentation, which separates vascular from nonvascular information, segmentation produces an output image where the pixels of the vasculature are represented by a value of one, and everything else by a value of zero. Even though vascular segmentation is critically important for quantitative vascular analysis, no existing study has examined how to validate a segmentation workflow in preclinical models such as zebrafish.
The main reasons for the lack of a robust and validated segmentation approach for the zebrafish cerebral vasculature are as follows:
- Most research on zebrafish vasculature has focused on vascular development in the trunk, as trunk vessel formation shows a highly stereotypic growth pattern that is well characterized.
- Although the zebrafish brain vasculature is increasingly studied, its complex topology can present significant technical and experimental challenges for visualizing all vessels at the same level of detail.
- As endothelial cells are visualized in transgenic lines, a cross-sectional double-peak intensity distribution is displayed in lumenized vessels, whereas a single-peak distribution occurs in small or unlumenized vessels (Kugler, Chico, & Armitage, 2018). This means any analysis approach needs to either (a) be able to detect and discriminate these or (b) include a processing step that ensures all vessels have a single- or double-peak distribution. This is of particular importance when working with vessels with highly different diameters (such as 2-60 µm), as applying filters at a single scale across such a range is rarely feasible.
- LSFM is a relatively new technique, with commercial microscopes becoming available only in recent years.
- Data acquisition with LSFM produces large datasets, requiring more computational resources for data handling, storage, and processing than other confocal imaging systems.
- Segmentation gold standards are lacking in preclinical models. In human medical imaging studies, segmentation gold standards usually take the form of expert manual measurements performed by a trained radiologist. However, there is no equivalent trained and qualified person in biological imaging. Additionally, due to the size and complexity of a zebrafish cranial vasculature dataset, extensive/accurate manual segmentation would be challenging and extremely time consuming (e.g., a single stack is typically around 1920 × 1920 × 400 voxels, in the x, y, and z directions, respectively).
- Phantom models that replicate the zebrafish cranial vasculature, which could provide an alternative gold standard for validation, are not available.
- Due to the lack of previously validated segmentation approaches, benchmarks to compare new methodological improvements are unavailable.
Previous Work Aiming to Quantify the Zebrafish Cerebral Vasculature
Quantification of vessels in the left hindbrain was previously performed by Tam et al. (2012), whereas Chen et al. (2012) presented quantification of midbrain vascular segments. Both methods used confocal microscopy data and focused on a subregion rather than the whole brain vasculature. Tam et al. (2012) measured the vascular density and diameter after deconvolution using the commercial software Imaris. Chen et al. (2012) quantified vessel length, branching hierarchy (Strahler, 1952), the existence of loops, and vascular pruning events using the commercial software Neurolucida. However, neither study provided sufficient methodological detail to replicate and perform an in-depth assessment of their performance.
Recently, a machine learning segmentation approach was presented for the whole zebrafish embryonic vasculature using LSFM data (Daetwyler, Günther, Modes, Harrington, & Huisken, 2019). The method was trained on data from double-transgenic zebrafish, providing endothelial as well as luminal signals to ensure its robustness for single- and double-peak vessel profiles. As an additional luminal signal (in this case a transgenic reporter line) is required to extract vascular information, the data load is doubled compared to that required for a single transgenic. Although this segmentation approach is promising, only visual assessment with no further validation of segmentation outcomes was performed.
Previously, Kugler and colleagues developed methods to enhance the cerebral vasculature in LSFM data using general filtering (GF) based on the application of median and rolling ball filters (Kugler et al., 2018) as well as by using a Hessian matrix–based enhancement, assuming local vessel tubularity, with the filter proposed by Sato and colleagues (Kugler, Plant, Chico, & Armitage, 2019; Sato et al., 1998). For the latter, local image gradients are described by the first image derivative and generalized into three dimensions by the Jacobian matrix, whereas the second derivative (change of gradient) is similarly represented by the Hessian matrix. To describe local curvature in the Hessian matrix, one can use nonzero vectors that change only by a scalar factor upon transformation, called eigenvectors (λ1, λ2, and λ3) and their respective magnitudes, i.e., eigenvalues (e1, e2, and e3). Using these eigenvectors and eigenvalues with the assumption that vessels are locally tubular/cylinder-like has inspired the development of vessel-specific filters to enhance vessel signals and reduce background. Two of the most widely used filters, originally developed for the medical field, are the Frangi filter (Frangi, Niessen, Vincken, & Viergever, 1998) and the Sato enhancement filter (Sato et al., 1998). The Sato enhancement filter uses the eigenvectors to enhance vessels assuming that vessels are locally a line, whereas the Frangi filter assumes them to be a tube. Sato enhancement is designed to use two eigenvalues to enhance tubes/lines, whereas the Frangi filter uses all three eigenvalues and considers sheets/plates, tubes/lines, and blobs/spheres. Additionally, the Frangi filter considers so called “ structureness ” describing gray level variations in images. Lastly, Frangi enhancement can work on dark vessels against a bright background and vice versa due to its use of absolute values, whereas Sato enhancement requires bright vessels against a dark background (for further information on mathematical definitions, the reader is referred to Frangi et al., 1998; Krissian, Malandain, & Ayache, 1998; Sato et al., 1998). Together, these vascular enhancement strategies are designed to increase contrast and gradient steepness between vascular and nonvascular signals prior to image segmentation. To this end, Kugler and colleagues (Kugler et al., 2019) investigated different image enhancement and subsequent segmentation methods, which were available in the open-source and widely-used Fiji image analysis software (Schindelin et al., 2012). These studies showed that for zebrafish brain vasculature data acquired with LSFM from fluorescent transgenic reporter lines, the best results were achieved applying Sato enhancement (Sato et al., 1998) at the scale of the examined vessels. This enhancement step was successfully followed by Otsu thresholding (Otsu, 1979) to achieve data binarization/segmentation, but again, no validation of the suggested approach was performed.
The above discussion proves that even though various approaches to segment the zebrafish brain vasculature exist, none have been validated and it is unclear how robust, sensitive, or accurate these approaches are. This lack of validation is particularly pressing as zebrafish are increasingly used to assess cerebrovascular changes upon disease, aging, and drug treatments (Bowley et al., 2021; Chico & Kugler, 2021). Thus, if segmentation approaches remain unvalidated, subtle biological phenotypes may be overlooked or falsely identified. Ideally, one would benchmark any new segmentation methodology against gold standard measurements covering a wide range of experimental situations including different vessel shapes, sizes, locations, data qualities/signal properties as well as image acquisition parameters acquired over a wide range of biological samples. As mentioned previously, expert manual segmentation is normally the accepted gold standard, but producing such data would be extremely time consuming, and it is unclear whether suitably qualified “experts” exist to perform such gold standard measurements. Therefore, comparing different segmentation methods can be used as a proxy to assess segmentation workflows.
Overview of Segmentation Validation Approaches
The lack of segmentation validation can be overcome by generating simulated data and manual measurements, along with studying datasets from groups subjected to experimental perturbation to challenge and assess segmentation performance. Below, we discuss different use cases that focus on the zebrafish cerebral vessels but describe approaches that can be widely used to assess segmentation outcomes when developing new segmentation workflows.
Together, this overview aims to (a) examine general approaches to assess segmentation quality and validate the suggested approaches, and (b) quantitatively address the lack of a segmentation gold standard for the zebrafish cerebrovascular architecture. The following are presented:
- As phantom models with realistic optical properties are lacking for the zebrafish brain vasculature, computer-simulated digital tube models with realistic cerebrovascular and imaging properties (diameter, edge properties, signal distribution, and noise) can be used as proxies to test analysis step responses. As the underlying properties of these tubes are known, enhancement and segmentation outcomes can be validated against these known parameters. Although computer-generated datasets are commonly studied in the medical field, they are used less often in biomedical image analysis. Using such data, we show how to understand and optimize the Sato enhancement filter (Sato et al., 1998).
- Although it is not feasible to obtain a segmentation gold standard for the zebrafish cerebrovascular system by manual segmentation (standard image size 1920 × 1920 × 400 voxels, in the x, y, and z directions, respectively), manual measurement of vessel diameters in a small number of selected vessels can be performed. When selecting the respective vessels, these should include the typical range encountered in the data and, if possible, be distributed equally across the dorsal-to-ventral as well as anterior-to-posterior axis. These diameter measurements can then be used as a “gold standard” and compared to automated measurements obtained after enhancement and segmentation to provide an estimate of the accuracy of the enhancement and segmentation procedure.
- Assessing segmentation performance should include not only segmentation robustness but also whether true biological effects can be detected. We discuss three approaches for this:
- To assess noise sensitivity, an experimental dataset with progressively decreasing image quality by controlled reduction of laser power, as quantified by the contrast-to-noise ratio (CNR), is produced. This dataset is further supplemented by a synthetic dataset generated with data augmentation.
- To assess segmentation sensitivity to true biological changes in the cerebral vessels, segmentation is performed on data acquired in the same animal before and after exsanguination, expecting that this will result in a decreased vascular volume.
- To further assess segmentation sensitivity, changes in the brain vascular volume during embryonic development from 3 to 5 days post fertilization (the standard way of referring to embryonic age) are quantified, as this is a period of growth and change that successful segmentation processes should detect.
- Even though general approaches to segmentation are often transferable to other types of datasets than those for which the approach was optimized, fine-tuning of individual steps, or parameters, is often required. Thus, to understand the generalizability of segmentation approaches, we demonstrate the degree to which segmentation developed for the transgenic Tg(kdrl:HRAS-mCherry)s916 , which has a high CNR (Kugler et al., 2019) and a vessel-specific expression pattern, could be applied to other transgenic lines, or whether further optimizations are required. The segmentation performance is assessed in the double-transgenic lines Tg(fli1a:eGFP)y1 , Tg(kdrl:HRAS-mCherry)s916 (Chi et al., 2008; Lawson & Weinstein, 2002), Tg(fli1a:CAAX-eGFP), Tg(kdrl:HRAS-mCherry)s916 (Gebala, Collins, Geudens, Phng, & Gerhardt, 2016), and Tg(fli1a:LifeAct-mClover)sh467, Tg(kdrl:HRAS-mCherry)s916 (Savage et al., 2019), as using double transgenics allows direct comparison of segmentation outcomes, and the four transgenics examined are generally widely used in laboratories around the world. This shows that the segmentation approach is indeed transferable with respect to extracting the brain vasculature, but that further processing/improvement is required to remove nonspecific signals, such as those from the skin.
- Lastly, due to the increasing importance and prevalence of deep learning (DL) methods in biological sciences, particularly in cerebrovascular segmentation of preclinical models (Daetwyler et al., 2019; Patera, Zippo, Bonnin, Stampanoni, & Biella, 2021; Todorov et al., 2020), there is a need to understand DL methods and their applicability to biomedical imaging data. We highlight several DL methods and show how these can be assessed against each other to understand their applicability and performance; specifically, the original U-Net (Ronneberger, Fischer, & Brox, 2015), SegNet (Badrinarayanan, Kendall, & Cipolla, 2017), and three modified versions of the original U-Net architecture (dU-Net). Overall, we conclude that DL methods are indeed applicable to the zebrafish brain vascular architecture and that comparing DL methods against each other is useful and practical.
To facilitate the uptake and understanding of segmentation validation methods, we share example data where appropriate at zenodo.org: Simulated Tubes and Filter Responses (doi: 10.5281/zenodo.5898012), Decreasing Contrast-To-Noise Ratio (doi: 10.5281/zenodo.5910316), Exsanguination (doi: 10.5281/zenodo.5914725), and Development (doi: 10.5281/zenodo.5914749.
Together, general approaches to validate segmentation workflows applicable beyond the presented use case of the zebrafish brain vasculature are demonstrated. We believe these will help biologists and image analysts develop unbiased segmentation validation approaches for a wide range of applications.
ENHANCEMENT OF FILTER OPTIMIZATION AND VALIDATION
One common approach in vascular segmentation is to use vascular enhancement to improve image quality prior to binarization/segmentation. As mentioned above, these enhancement methods typically assume that vessels are locally a tube, i.e., a circular or ellipsoidal cross section that extends axially to form a tube. This shape-based assumption has led to various filters that enhance vessels relative to other structures, provided they have the expected tube-like properties, as is the case for the Sato, Frangi (Frangi et al., 1998, 1999; Sato et al., 1998), and other filters. However, these were traditionally implemented for clinical imaging modalities such as magnetic resonance imaging (MRI) where vascular contents are visualized. In this case, the vessel cross-sectional intensities are single peaks with radial Gaussian-like distributions. This contrasts with biomedical image analysis, such as zebrafish transgenic reporter lines or mouse antibody stainings, where the cells that make up the vessel walls—called endothelial cells —are visualized (Kugler et al., 2018; Todorov et al., 2020). This leads to a cross-sectional double-peak (or ring-shaped signal) intensity distribution in lumenized vessels, whereas unlumenized (often very small) vessels display single peaks (Kugler et al., 2018; Todorov et al., 2020). Although this could be addressed experimentally by performing microangiography, this is (a) laborious and (b) only shows perfused vessels. Thus, when applying vessel enhancement filters, one has to remember that these were implemented in clinical imaging rather than in fluorescence microscopy, i.e., for data with highly different signal properties and signal distributions.
Despite these major differences in data properties compared to the traditional applications where vessel content is imaged, the Sato enhancement (SE) filter—the filter that enhances lines/tubes based on eigenvectors—was previously shown to improve the quality of LSFM data from the zebrafish brain vasculature; this was quantified by the vessel-to-background CNR when applied at a scale size similar to the average vessel size. Moreover, in this work, approaches to measure CNR in the brain vasculature were demonstrated, and CNR measurements were generally found suitable for measuring the applicability of filters (Kugler et al., 2019).
In addition to CNR measurements, other vascular and image properties that enable assessment of filter responses include vessel diameters, edge properties, signal distribution, and noise. For example, to study the filter response at various vessel diameters, one can compare in vivo data from vessels with different diameters located at different anatomical positions throughout the brain, as exemplified in Figure 1A. When applying filters, these same vessels can be used to demonstrate the applicability of the filters, as shown here for SE, that successfully enhanced the displayed vessels (Fig. 1A′). A “successful” vessel enhancement filter is generally defined as the one that results in decreased background noise, more homogenous signals across the vessel, and an increased vessel-to-background CNR. To study the implementation of enhancement filters, image inversion can be used (Fig. 1B); for example, the theoretical assumption regarding SE is that it is only effective for bright vessels with a dark background. However, as computational implementations can differ from the original mathematical framework, testing both (dark-on-bright and bright-on-dark) scenarios can be useful. In this example, as expected, SE fails to perform vessel enhancement on inverted images (Fig. 1B). Together, these tests show that the examined filter meaningfully enhances vessel enhancement, provided data are presented as bright-on-dark and applied at the scale of the desired vessels.
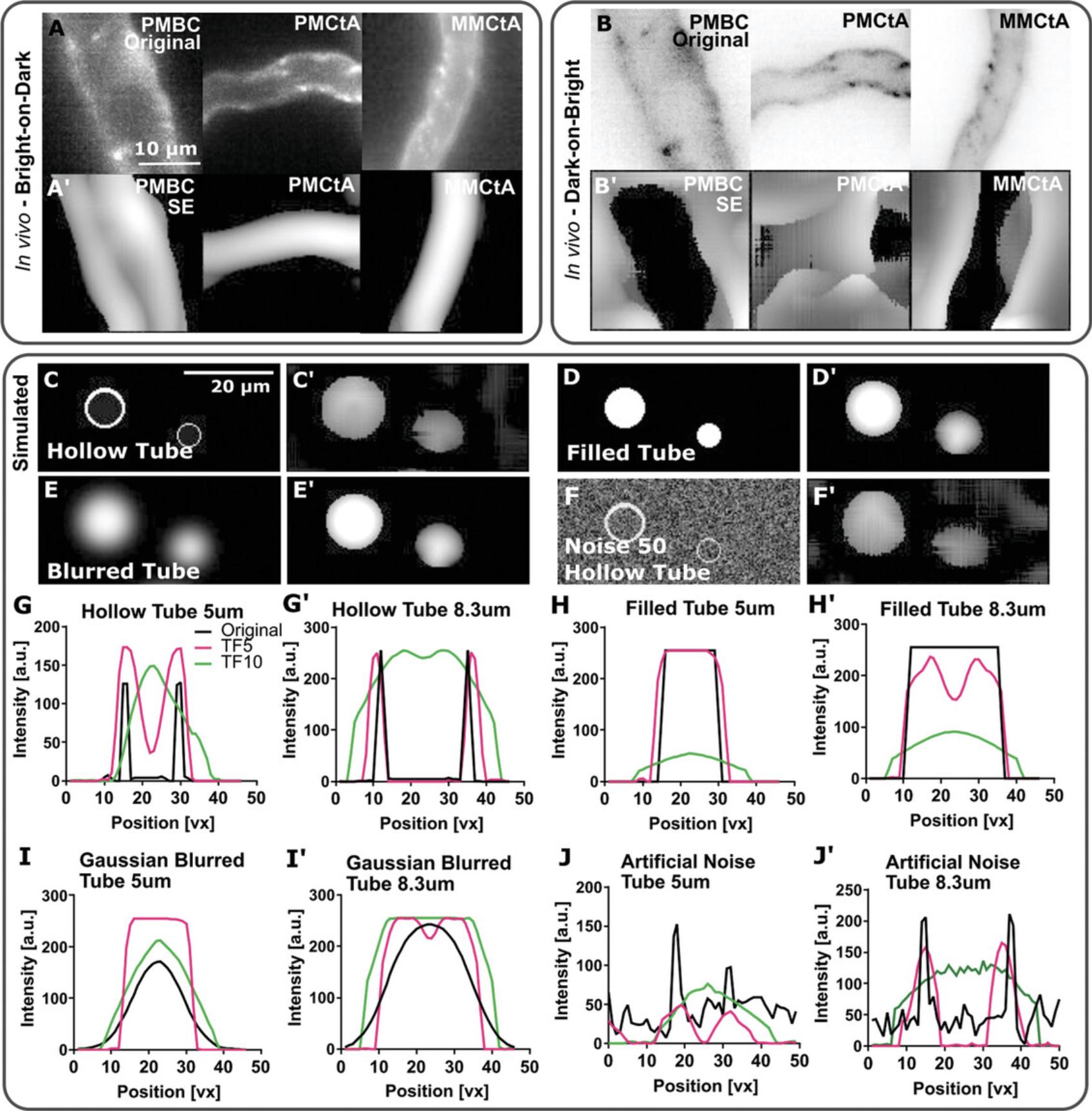
Vessel filters and subsequent segmentation outcomes are also affected by the input vessel shape and lumenization status:
- Lumenized, i.e., hollow tubes with double-peak intensity
- Unlumenized/unperfused, i.e., filled tubes with single-peak intensity
To test this, modeled tubes resembling the observed data can be produced computationally to create relevant “digital phantoms.” These enable the study of filter impacts on vessels of different diameters, intensity distributions, and varying noise levels (see Materials and Methods for simulated tube details). Once simulated tubes are created, the filter of interest can then be applied to study the filter outputs visually using line ROIs to plot cross-sectional intensity distributions. For the use case presented here, SE was applied to simulated hollow tubes. Examining the filter outcomes revealed that SE converted the tubes to filled tubes (conversion from double- to single-peak) upon enhancement at a scale approximately equal to the size of tubes (10 µm; Fig. 1C), suggesting that filled and unfilled vessels would be filtered similarly. The results obtained after enhancement of filled and filled Gaussian-blurred tubes were similar (Fig. 1D and 1E). Lastly, the addition of artificial Gaussian noise to the input images did not significantly affect enhancement (Fig. 1F), indicating the noise robustness of the filter. Together, such digital phantoms allow users to predict how filters might impact input data and whether satisfactory enhancement can be achieved before segmentation. These filters improve image quality, and the tubes can be considered “ filled ” following the enhancement step, thus making unlumenized and lumenized vessels equal for subsequent steps.
Other approaches could be to artificially fill all vessels after segmentation (i.e., a 3D hole-filling approach) or create vascular surfaces from the segmented objects and work with “empty” vessels. In essence, for quantification of vascular shapes or centerline extraction, vessels should have the same features (i.e., filled or unfilled), independent of the scale or properties, to allow all vessels to be analyzed in an unbiased fashion.
To gain further insight in an unbiased manner, cross-sectional intensity profiles can be plotted using line ROIs. For the presented use case, these profiles show that hollow-tube single-peak conversion is achieved when the filter is applied with the scale parameter at or larger than the tube diameter (Fig. 1G); however, filtering at a smaller scale leads to an increased edge response, with external and internal tube edges observed for tubes with double peak/ring profiles. This edge response increased upon filtering with a smaller sigma and was also observed for the other examined tubes (Fig. 1H-J). Thus, plotting cross-sectional intensity distributions before and after filtering provides additional insights into filter responses that might be overlooked upon visual data assessment.
By examining simulated tubes that are blurred and have additional noise, one can examine how filters respond to input data that more closely mimic the experimental data. As seen from the images and intensity profiles in Figure 1, there is a tendency for the simulated tube width to appear broader after enhancement. Any subsequent segmentation would need to be tuned for the correct vessel width (i.e., if there is a global and reproducible broadening during the enhancement step, this can be rectified during segmentation). It is important to note that when examining data in other vascular beds or species, where vascular diameters and signal profiles are different and possibly more variable than those in the zebrafish brain, alternative simulations would be required to ensure that the digital phantoms used to optimize the enhancement process represent the expected experimental data. This is likely to be the case when working with vessels spanning a large size range where multiple scales need to be integrated. Further details are available elsewhere (Chang, Huynh, Vazquez, & Salafia, 2013).
SEGMENTATION VALIDATION
Following image enhancement, the typical next step is image segmentation to binarize images for subsequent quantification. As there are a plethora of segmentation approaches, their discussion goes beyond the scope of this review; further information is available elsewhere (Khan, 2014; Kirbas & Quek, 2004; Lesage, Angelini, Bloch, & Funka-Lea, 2008; Moccia, De Momi, El Hadji, & Mattos, 2018; Renard, Guedria, Palma, & Vuillerme, 2020).
Before comprehensively discussing how to assess and validate a segmentation approach, we briefly want to touch upon two methods to assess the applicability of rapid segmentation to data: (a) visual assessment and (b) quantification using similarity metrics. We present examples using the open-source software Fiji, but the general approaches equally apply to other image analysis software.
For visual assessment , it often suffices to observe the segmented data to determine whether over- (a nonvascular pixel classified as a vascular pixel, i.e., false positive) or undersegmentation (vascular pixels classified as background noise, i.e., false negative) occurred. Overlapping original images with segmented data is generally a suitable visual approach (e.g., Fiji: Image > Color > Merge Channels > select: C1 original and C2 segmented image). Examining data in detail and exploring them in 3D enables researchers to gauge whether, for example, there are global segmentation errors or whether certain regions are not well segmented.
For quantification using similarity metrics , there are two steps to be examined: (i) the Fiji MorpholibJ Plugin (Legland, Arganda-Carreras, & Andrey, 2016), which allows quantification of image pixel overlap parameters such as the Dice coefficient, Jaccard index, or total pixel overlap; or (ii) comparing image similarity parameters such as the sum of squared differences (SSD), sum of absolute differences (SAD), maximum absolute difference (MAD), mean square error (MSE), structural similarity (SSI), or mutual information (MI) (Matlab code: https://github.com/ElisabethKugler/Matlab3D-ImageAnalysis/tree/main/ImageSimilarityMeasurement).
Following these initial assessments, if the method appears to deliver a satisfactory enhancement and segmentation workflow, one can start to think about validating the approach more thoroughly. In the following sections, approaches to evaluate segmentation accuracy, robustness to noise, sensitivity to biological differences, and examinations of biological data (e.g., developmental data or different transgenic lines) are explored.
Segmentation accuracy
To identify whether a segmentation workflow is effective across the expected range of cerebral vessel sizes, segmentation accuracy has to be evaluated. This can be achieved by measuring vessel diameters after application of the enhancement and segmentation step and comparing those to the “gold standard” manual measurements. To gain additional insights into the role of image enhancement, different enhancement/segmentation workflows can be compared against each other. To showcase a comparative approach here, we compare data filtered with general [GF; median and rolling ball filters (Kugler et al., 2018)] or SE filters before segmentation, again using zebrafish brain vasculature data acquired with LSFM in the stable transgenic Tg(kdrl:HRAS-mCherry)s916 (Chi et al., 2008).
The first step is to establish a gold standard via manual measurements. Ideally, vessels spanning the full range of diameters observed in the data should be used; in the case of the zebrafish brain vasculature, this is 5-20 μm. Four vessels were chosen: the central artery (CtA), average diameter of 8.154±1.27 µm; the middle mesencephalic central artery (MMCtA), average diameter of 9.78±2.09 µm; the primordial midbrain channel (PMBC), average diameter of 11.14±1.68 µm; and the basilar artery (BA), average diameter of 22.28±3.89 µm (n = 12; 3 dpf embryos). Importantly, selection of vessels will differ for different ages, vascular beds, visualizations (e.g., transgenics, or antibody stainings), or species, depending on the intended application.
As manual measurements are laborious and prone to bias, the full width at half-maximum (FWHM; code: https://github.com/ElisabethKugler/Matlab3D-ImageAnalysis/tree/main/ImageProcessingTests) of the cross-sectional intensity profile of the vessel is often used in the medical field to estimate the vessel diameter automatically. As this is less widely applied to preclinical models, comparing FWHM to the manual diameter measurements should provide meaningful insights into the overall applicability. We found no statistically significant differences (Fig. 2A; all vessels p > 0.9999) or error rates (CtA 1.44 µm, MMCtA 0.91 µm, PMBC 1.35 µm, and BA 3.83 µm). Using additional measures, such as Pearson Correlation and Bland-Altman analyses, can provide further insights into systematic errors that might otherwise be overlooked. When examining data, outliers might be encountered (Fig. 2A; unfilled arrowhead) and potential causes identified. For example, strong asymmetric cross-sectional intensity distributions (Fig. 2B) could lead to FWHM bias. Identifying this could then inform whether outlier exclusion is required or whether, for example, multidirectional FHWM measurement and averaging are needed; alternative approaches for vessel diameter measurements could be applied to address outliers (see reviews: Corliss, Mathews, Doty, Rohde, & Peirce, 2019; Lidayová, Frimmel, Wang, Bengtsson, & Smedby, 2017).
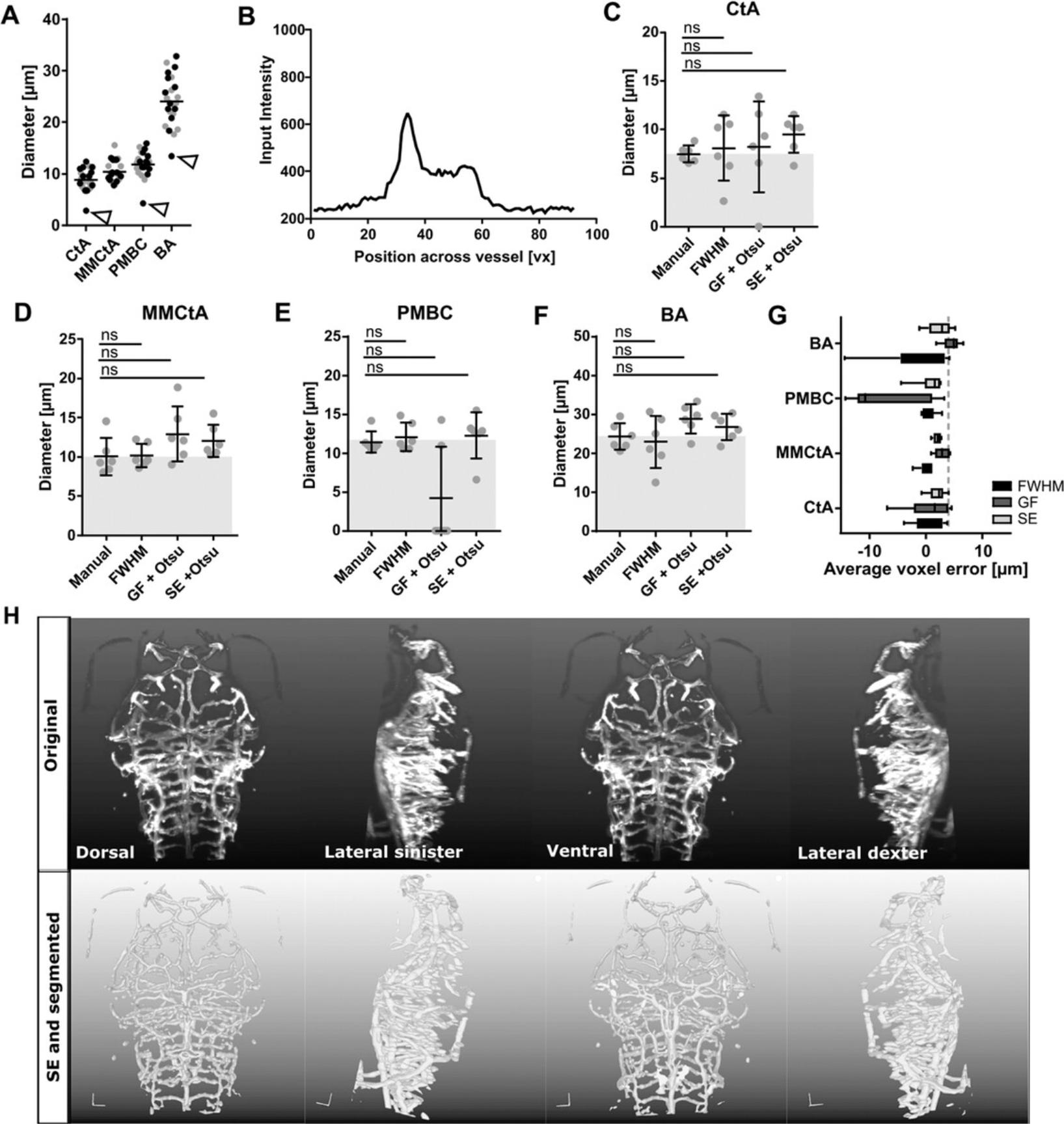
To further compare the impact of filters, estimates of the vascular diameters derived manually and using FWHM in original images can be compared with those derived from GF and SE after Otsu thresholding. This helps understand whether FWHM-, GF-, or SE-based diameter measurements and the corresponding manual measurements are comparable. Additionally, analyzing the intragroup coefficient of variation (CoV) provides insight into data variability. For example, in the data shown here, SE delivered more consistent results (Fig. 2C-G; CoV MMCtA manual 24%, FWHM 15%, GF 28%, and SE 17%; CoV CtA manual 11%, FWHM 42%, GF 57%, and SE 20%; CoV PMBC manual 12%, FWHM 42%, GF 57%, and SE 24%; CoV BA manual 14%, FWHM 29%, GF 13%, and SE 12%). Together with visual assessment (Fig. 2G-H; Videos 1 and 2), these steps indicate whether a segmentation workflow introduces artificial bias.
CONCLUDING REMARKS
In this work, steps toward developing and validating a segmentation workflow were demonstrated, with the zebrafish brain vasculature as a use case. Our overview covered various techniques to validate the robustness, sensitivity, and accuracy of segmentation workflows, including synthetic tubes, experimental data, and augmented experimental data, paired with comparative approaches. For studying enhancement and segmentation, FWHM is appropriate to quantify local vessel diameters in the data examined here, similar to data acquired with medical imaging modalities (Merkx et al., 2012; Varma, Subramanyan, & Durgan, 2004). Furthermore, we discussed visual and quantitative assessments (e.g., CoV, Dice coefficient, and Bland-Altman ratio) of segmentations with general and DL approaches.
Segmentation Validation and Benchmark Datasets
Using manual measurements, comparisons of segmentation methods, and purpose-built datasets (i.e., varying CNR levels, exsanguination, development, and double transgenics), an objective way to examine and validate segmentation workflows can be established. Considering that phantom models and segmentation benchmarks are still widely lacking in biomedical sciences, a multilevel validation approach is a meaningful way to deliver reliable biomedical image analysis workflows. Together, this overview provides a proof of principle on how experimental, simulated, and analytical approaches can be combined to assess analysis workflows in biomedical image analysis, as was previously shown for medical image analysis (Kirişli et al., 2013). Once such segmentation validation is established, this allows these measurements to be used as benchmarks to test against other enhancement and segmentation workflows. However, application to other ages, vascular beds, visualization techniques, or species will require further optimization.
Segmentation Transferability to Other Visualization Techniques in Zebrafish Embryos
As most segmentation workflows are developed for one specific reporter line, segmentation transferability to other transgenic reporter lines requires further attention, as transferability studies have never been conducted. Using the concept of double transgenics or double markers is a valuable approach for examining segmentation outcomes as well as identifying/confirming optimal markers. For example, in our use case, we found that nonvascular signals (pan-endothelial) as well as nonspecific (e.g., skin) signals lead to a quantifiable increase in the extracted vascular volume. These examples show that direct segmentation transferability is unlikely but that improvements are required, and these could be at various levels such as image preprocessing to enhance vascular and decrease nonvascular signals, exclusion of unconnected components, exclusion of objects under a specified size threshold, or exclusion based on the peripheral position. Similarly, DL approaches can take advantage of advances in the field of transfer learning, where previously optimized networks are efficiently retrained for additional applications.
Future work could build on this by (a) studying data visualized with microangiography (in vivo , visualizing only perfused vessels) or immunohistochemistry (fixed tissue, visualizing whole vasculature), or (b) examining data acquired with other techniques, such as confocal microscopy [significant signal decay along the z axis (Tröger et al., 2020)]. Importantly, even though SE was developed for MRI data, transferability to transgenic reporter line data acquired with LSFM does exist. Thus, there is no reason to believe that it cannot be further optimized to data with similar properties such as lymphatics or other networks with tubular structures.
DL-based segmentation
Overall, although DL-based segmentation delivered good segmentation outcomes, segmentation validation steps showed that there was a tendency toward systematic overestimation of the vascular volume, highlighting that segmentation validation is pivotal. We demonstrate in this overview that although, or maybe even because, DL is a widely emerging field, more work is needed that examines segmentation validation, and that end-user interpretation is needed to assess the suitability for segmentation applications to everyday data.
However, even if a segmentation approach is optimized or trained on a particular dataset, transferability to other datasets should not be assumed. Thus, further work is needed to examine the performance of DL-based segmentation on datasets across samples at different ages, in different transgenic lines, and in images with varying image qualities.
In conclusion, we studied zebrafish cerebrovascular segmentation methods and provided approaches to validate the segmentation workflows in the absence of a gold standard. Using simulated, experimental, and augmented datasets allowed us to demonstrate segmentation accuracy, sensitivity, and robustness. Building on this, we could establish that a segmentation workflow optimized for a specific visualization approach (e.g., particular reporter line or antibody staining) has limited generalizability, and optimization for its application to other data is critical. Lastly, the use of different DL networks showed that a comparative approach using quantitative assessments enables segmentation validation.
Importantly, the application of robust objective segmentation allows for the reduction of the sample size needed to assess the vascular phenotype, which is important from an ethical as well as a computational point of view.
AUTHOR CONTRIBUTIONS
Elisabeth C. Kugler : conceptualization, data curation, formal analysis, methodology, project administration, software, validation, visualization, writing original draft, writing review and editing; Andrik Rampun : methodology, software, writing original draft; Timothy J.A. Chico : conceptualization, funding acquisition, project administration, resources, supervision, visualization, writing review and editing; Paul A. Armitage : conceptualization, funding acquisition, methodology, project administration, resources, supervision, writing review and editing.
CONFLICT OF INTEREST
The authors declare no conflict of interest.
Open Research
DATA AVAILABILITY STATEMENT
Example data were shared as appropriate at zenodo.org: Simulated Tubes and Filter Responses (doi: 10.5281/zenodo.5898012), Decreasing Contrast-To-Noise Ratio (doi: 10.5281/zenodo.5910316), Exsanguination (doi: 10.5281/zenodo.5914725), and Development (doi: 10.5281/zenodo.5914749).
Supporting Information
| Filename | Description |
|---|---|
| cpz1443-sup-0001-FigureS1.tif7.5 MB | Suppinfo |
| cpz1443-sup-0001-SuppMat.docx46 KB | Suppinfo |
Please note: The publisher is not responsible for the content or functionality of any supporting information supplied by the authors. Any queries (other than missing content) should be directed to the corresponding author for the article.
LITERATURE CITED
- Abdar, M., Pourpanah, F., Hussain, S., Rezazadegan, D., Liu, L., Ghavamzadeh, M., … Nahavandia, S. (2021). A review of uncertainty quantification in deep learning: Techniques, applications and challenges. Information Fusion , 76, 243–297. doi: 10.1016/j.inffus.2021.05.008.
- Badrinarayanan, V., Kendall, A., & Cipolla, R. (2017). SegNet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence , 39, 2481–2495. doi: 10.1109/TPAMI.2016.2644615.
- Bland, J. M., & Altman, D. G. (1986). Statistical methods for assessing agreement between two methods of clinical measurement. Lancet , 1, 307–310. doi: 10.1016/S0140-6736(86)90837-8.
- Bowley, G., Kugler, E., Wilkinson, R., Lawrie, A., van Eeden, F., Chico, T. J. A., … Serbanovic-Canic, J. (2021). Zebrafish as a tractable model of human cardiovascular disease. British Journal of Pharmacology , 179, 900–917. doi: 10.1111/bph.15473.
- Brownlee, J. (2018). How to configure the number of layers and nodes in a neural network. Available at: https://machinelearningmastery.com/how-to-configure-the-number-of-layers-and-nodes-in-a-neural-network/.
- Chang, J.-M., Huynh, N., Vazquez, M., & Salafia, C. (2013). Vessel enhancement with multiscale and curvilinear filter matching for placenta images, pp. 125–128. In 2013 20th International Conference on Systems, Signals and Image Processing (IWSSIP).
- Chen, Q., Jiang, L., Li, C., Hu, D., Bu, J., Cai, D., & Du, J. (2012). Haemodynamics-driven developmental pruning of brain vasculature in zebrafish. PLoS Biology , 10, e1001374. doi: 10.1371/journal.pbio.1001374.
- Chi, N. C., Shaw, R. M., De Val, S., Kang, G., Jan, L. Y., Black, B. L., & Stainier, D. Y. R. (2008). Foxn4 directly regulates tbx2b expression and atrioventricular canal formation. Genes & Development, 22, 734–739.
- Chicco, D. (2017). Ten quick tips for machine learning in computational biology. BioData Mining , 10, 35. doi: 10.1186/s13040-017-0155-3.
- Chico, T. J. A., & Kugler, E. C. (2021). Cerebrovascular development: Mechanisms and experimental approaches. Cellular and Molecular Life Sciences , 78(9), 4377–4398. doi: 10.1007/s00018-021-03790-1.
- Chico, T. J. A., Ingham, P. W., & Crossman, D. C. (2008). Modeling cardiovascular disease in the zebrafish. Trends in Cardiovascular Medicine , 18, 150–155. doi: 10.1016/j.tcm.2008.04.002.
- Corliss, B. A., Mathews, C., Doty, R., Rohde, G., & Peirce, S. M. (2019). Methods to label, image, and analyze the complex structural architectures of microvascular networks. Microcirculation , 26, e12520. doi: 10.1111/micc.12520.
- Daetwyler, S., Günther, U., Modes, C. D., Harrington, K., & Huisken, J. (2019). Multi-sample SPIM image acquisition, processing and analysis of vascular growth in zebrafish. Development , 146(6), dev173757. doi: 10.1242/dev.173757.
- Feigin, V. L., Norrving, B., & Mensah, G. A. (2017). Global burden of stroke. Circulation Research , 120, 439–448. doi: 10.1161/CIRCRESAHA.116.308413.
- Frangi, A. F., Niessen, W. J., Vincken, K. L., & Viergever, M. A. (1998). Multiscale vessel enhancement filtering, pp. 130–137. In Medical image computing and computer-assisted intervention—MICCAI’98. Springer.
- Frangi, A. F., Niessen, W. J., Hoogeveen, R. M., van Walsum, T., & Viergever, M. A. (1999). Model-based quantitation of 3-D magnetic resonance angiographic images. IEEE Transactions on Medical Imaging , 18, 946–956. doi: 10.1109/42.811279.
- Gebala, V., Collins, R., Geudens, I., Phng, L.-K., & Gerhardt, H. (2016). Blood flow drives lumen formation by inverse membrane blebbing during angiogenesis in vivo. Nature Cell Biology , 18, ncb3320. doi: 10.1038/ncb3320.
- Greener, J. G., Kandathil, S. M., Moffat, L., & Jones, D. T. (2022). A guide to machine learning for biologists. Nature Reviews Molecular Cell Biology , 23, 40–55. doi: 10.1038/s41580-021-00407-0.
- Gut, P., Reischauer, S., Stainier, D. Y. R., & Arnaout, R. (2017). Little fish, big data: zebrafish as a model for cardiovascular and metabolic disease. Physiological Reviews , 97, 889–938. doi: 10.1152/physrev.00038.2016.
- Huisken, J., Swoger, J., Del Bene, F., Wittbrodt, J., & Stelzer, E. H. K. (2004). Optical sectioning deep inside live embryos by selective plane illumination microscopy. Science , 305, 1007–1009. doi: 10.1126/science.1100035.
- Khan, M. W. (2014). A survey: Image segmentation techniques. International Journal of Future Computer and Communication; Singapore , 3, 89–93. doi: 10.7763/IJFCC.2014.V3.274.
- Kirbas, C., & Quek, F. (2004). A review of vessel extraction techniques and algorithms. ACM Computing Surveys , 36, 81–121. doi: 10.1145/1031120.1031121.
- Kirişli, H. A., Schaap, M., Metz, C. T., Dharampal, A. S., Meijboom, W. B., Papadopoulou, S. L., … van Walsum, T. (2013). Standardized evaluation framework for evaluating coronary artery stenosis detection, stenosis quantification and lumen segmentation algorithms in computed tomography angiography. Medical Image Analysis , 17, 859–876. doi: 10.1016/j.media.2013.05.007.
- Kirst, C., Skriabine, S., Vieites-Prado, A., Topilko, T., Bertin, P., Gerschenfeld, G., … Renier, N. (2020). Mapping the fine-scale organization and plasticity of the brain vasculature. Cell , 180, 780–795.e25. doi: 10.1016/j.cell.2020.01.028.
- Krissian, K., Malandain, G., & Ayache, N. (1998). Model based multiscale detection and reconstruction of 3D vessels. INRIA. Available at https://hal.inria.fr/inria-00073248/document.
- Kugler, E., Chico, T., & Armitage, P. (2018). Image analysis in light sheet fluorescence microscopy images of transgenic zebrafish vascular development. In M. Nixon, S. Mahmoodi, & R. Zwiggelaar (Eds.), Medical image understanding and analysis. MIUA 2018 (pp. 343–353). Cham, Germany: Springer.
- Kugler, E., Plant, K., Chico, T., & Armitage, P. (2019). Enhancement and segmentation workflow for the developing zebrafish vasculature. Journal of Imaging , 5, 14. doi: 10.3390/jimaging5010014.
- Kugler, E. C., Frost, J., Silva, V., Plant, K., Chhabria, K., Chico, T. J. A., & Armitage, P. A. (2022). Zebrafish Vascular Quantification (ZVQ): A tool for quantification of three-dimensional zebrafish cerebrovascular architecture by automated image analysis. Development , 149(3), dev199720. doi: 10.1242/dev.199720.
- Lackland, D. T., & Weber, M. A. (2015). Global burden of cardiovascular disease and stroke: Hypertension at the core. Canadian Journal of Cardiology , 31, 569–571. doi: 10.1016/j.cjca.2015.01.009.
- Lawson, N. D., & Weinstein, B. M. (2002). In vivo imaging of embryonic vascular development using transgenic zebrafish. Developmental Biology , 248, 307–318. doi: 10.1006/dbio.2002.0711.
- LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature , 521, 436–444. doi: 10.1038/nature14539.
- Legland, D., Arganda-Carreras, I., & Andrey, P. (2016). MorphoLibJ: Integrated library and plugins for mathematical morphology with ImageJ. Bioinformatics , 32, 3532–3534.
- Lesage, D., Angelini, E. D., Bloch, I., & Funka-Lea, G. (2008). Medial-based Bayesian tracking for vascular segmentation: Application to coronary arteries in 3D CT angiography, pp. 268–271. In 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro.
- Lidayová, K., Frimmel, H., Wang, C., Bengtsson, E., & Smedby, Ö. (2017). Chapter 12: Skeleton-based fast, fully automated generation of vessel tree structure for clinical evaluation of blood vessel systems. In P. K. Saha, G. Borgefors, & G. Sanniti di Baja (Eds.), Skeletonization-theory, methods and applications. Cambridge, Massachusetts: Academic Press.
- Lindsey, B. W., Douek, A. M., Loosli, F., & Kaslin, J. (2018). A whole brain staining, embedding, and clearing pipeline for adult zebrafish to visualize cell proliferation and morphology in 3-dimensions. Frontiers in Neuroscience , 11, 750. doi: 10.3389/fnins.2017.00750.
- Litjens, G., Kooi, T., Bejnordi, B. E., Setio, A. A. A., Ciompi, F., Ghafoorian, M., … Sánchez, C. I. (2017). A survey on deep learning in medical image analysis. Medical Image Analysis , 42, 60–88. doi: 10.1016/j.media.2017.07.005.
- Merkx, M. A. G., Bescós, J. O., Geerts, L., Bosboom, E. M. H., van de Vosse, F. N., & Breeuwer, M. (2012). Accuracy and precision of vessel area assessment: Manual versus automatic lumen delineation based on full-width at half-maximum. Journal of Magnetic Resonance Imaging , 36, 1186–1193. doi: 10.1002/jmri.23752.
- Miyawaki, T., Morikawa, S., Susaki, E. A., Nakashima, A., Takeuchi, H., Yamaguchi, S., … Ikegaya, Y. (2020). Visualization and molecular characterization of whole-brain vascular networks with capillary resolution. Nature Communications , 11, 1104. doi: 10.1038/s41467-020-14786-z.
- Moccia, S., De Momi, E., El Hadji, S., & Mattos, L. S. (2018). Blood vessel segmentation algorithms—Review of methods, datasets and evaluation metrics. Computer Methods and Programs in Biomedicine , 158, 71–91. doi: 10.1016/j.cmpb.2018.02.001.
- Moen, E., Bannon, D., Kudo, T., Graf, W., Covert, M., & Van Valen, D. (2019). Deep learning for cellular image analysis. Nature Methods , 16, 1233–1246. doi: 10.1038/s41592-019-0403-1.
- Otsu, N. (1979). A threshold selection method from gray-level histograms. IEEE Transactions on System Man Cybernetics , 9, 62–66. doi: 10.1109/TSMC.1979.4310076.
- Patera, A., Zippo, A. G., Bonnin, A., Stampanoni, M., & Biella, G. E. M. (2021). Brain micro-vasculature imaging: An unsupervised deep learning algorithm for segmenting mouse brain volume probed by high-resolution phase-contrast X-ray tomography. International Journal of Imaging Systems and Technology , 31, 1211–1220. doi: 10.1002/ima.22520.
- Pestel, G. J., Hiltebrand, L. B., Fukui, K., Cohen, D., Hager, H., & Kurz, A. M. (2006). Assessing intravascular volume by difference in pulse pressure in pigs submitted to graded hemorrhage. Shock , 26, 391–395. doi: 10.1097/01.shk.0000228792.10550.ed.
- Renard, F., Guedria, S., Palma, N. D., & Vuillerme, N. (2020). Variability and reproducibility in deep learning for medical image segmentation. Scientific Reports , 10, 13724. doi: 10.1038/s41598-020-69920-0.
- Ronneberger, O., Fischer, P., & Brox, T. (2015). U-Net: Convolutional networks for biomedical image segmentation. In N. Navab, J. Hornegger, W. M. Wells, & A. F. Frangi (Eds.), Medical image computing and computer-assisted intervention–MICCAI 2015 (pp. 234–241). Cham, Germany: Springer International Publishing.
- Sato, Y., Nakajima, S., Atsumi, H., Koller, T., Gerig, G., Yoshida, S., & Kikinis, R. (1998). 3D multi-scale line filter for segmentation and visualization of curvilinear structures in medical images. In CVRMed-MRCAS’97 (pp. 213–222). Berlin, Heidelberg: Springer.
- Savage, A. M., Kurusamy, S., Chen, Y., Jiang, Z., Chhabria, K., MacDonald, R. B., … Wilkinson, R. N. (2019). tmem33 is essential for VEGF-mediated endothelial calcium oscillations and angiogenesis. Nature Communications , 10, 732. doi: 10.1038/s41467-019-08590-7.
- Schindelin, J., Arganda-Carreras, I., Frise, E., Kaynig, V., Longair, M., Pietzsch, T., … Cardona, A. (2012). Fiji—an open-source platform for biological image analysis. Nature Methods , 9, 676–682. doi: 10.1038/nmeth.2019.
- Sehnert, A. J., Huq, A., Weinstein, B. M., Walker, C., Fishman, M., & Stainier, D. Y. R. (2002). Cardiac troponin T is essential in sarcomere assembly and cardiac contractility. Nature Genetics , 31, 106–110. doi: 10.1038/ng875.
- Strahler, A. N. (1952). Dynamic basis of geomorphology. GSA Bulletin , 63, 923–938. doi: 10.1130/0016-7606(1952)63%5b923:DBOG%5d2.0.CO;2.
- Tam, S. J., Richmond, D. L., Kaminker, J. S., Modrusan, Z., Martin-McNulty, B., Cao, T. C., … Watts, R. J. (2012). Death receptors DR6 and TROY regulate brain vascular development. Developmental Cell , 22, 403–417. doi: 10.1016/j.devcel.2011.11.018.
- Todorov, M. I., Paetzold, J. C., Schoppe, O., Tetteh, G., Shit, S., Efremov, V., … Ertürk, A. (2020). Machine learning analysis of whole mouse brain vasculature. Nature Methods , 17, 442–449. doi: 10.1038/s41592-020-0792-1.
- Tröger, J., Hoischen, C., Perner, B., Monajembashi, S., Barbotin, A., Löschberger, A., … Hemmerich, P. (2020). Comparison of multiscale imaging methods for brain research. Cells , 9, 1377. doi: 10.3390/cells9061377.
- van Iterson, M., van Haagen, H. H. H. B.M., & Goeman, J. J. (2012). Resolving confusion of tongues in statistics and machine learning: A primer for biologists and bioinformaticians. Proteomics , 12, 543–549. doi: 10.1002/pmic.201100395.
- Varma, J. K., Subramanyan, K., & Durgan, J. (2004). Full width at half maximum as a measure of vessel diameter in computed tomography angiography. In Medical imaging 2004: Image perception, observer performance, and technology assessment (pp. 447–454). International Society for Optics and Photonics.

